Does music training improve other academic skills?

One sometimes hears the inclusion of music in the curriculum justified by the claim that it improves mathematics, or reading.

I’ve never cared for this justification because I think students should study music for its own sake, whether or not it boosts other skills. And it seems a chancy argument; if it turns out that music doesn’t help other academic work, does that mean it should be dumped?

Setting that argument aside, it’s certainly of interest from a cognitive point of view to know whether musical training has an impact on reading or math. There are a good number of correlational studies showing a positive effect, but few experimental data.

Now a new experimental study (Rautenberg, in press) shows that music training does have some positive effect for reading.

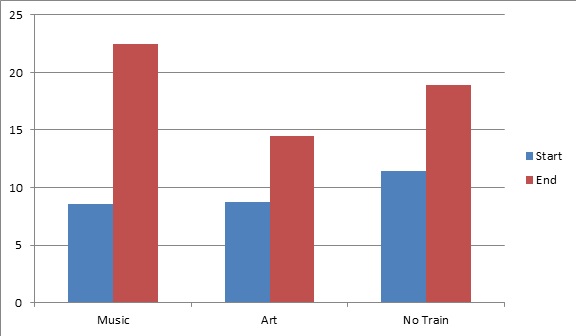
159 German 1st graders participated. The music training lasted 8 months and focused on three areas: rhythmic skills training, tonal/melodic skills training and auditory discrimination of timbre and sound intensity. There were two control groups: one received no training. The other was an active control receiving  training in art.

The results were fairly robust, as shown in the graph of single word reading accuracy at the beginning and end of the year.

What’s behind the benefit? Language does have a musical aspect to it, referred to as prosody. And indeed, children’s ability to appreciate the rhythmic aspect of speech is correlated with the ease with which they learn to read, even when controlling for phonemic awareness. In German (and in English) certain letter combinations signal certain stress patterns, so there is a signal in the written language that children can learn. The ideas is that children are less likely to learn the association of certain written letter patterns and their corresponding rhythms in speech if they don’t perceive the rhythms of speech very well.

That’s the argument. More fine-grained analyses of the data partially support it.

The argument predicts that it’s rhythm that’s important, not tonality, and the data do show significant correlations of reading with ability in the former, but not the latter.

The argument further predicts that the training ought to reduce a particular type of error: one in which a child reads the phonetic sounds correctly but gets the rhythm wrong; they segment the word into syllables incorrectly, or they accent the wrong syllable. This prediction was not supported.

All in all, this study seems to be an important addition--although certainly not a conclusive one--to the argument that some types of music training aids children's learning to read, at least in certain languages.

Reference
Rautenberg, I. (in press). The effects of musical training on the decoding skills of German-speaking primary school children. Journal of Research in Reading.

Which of these learning situations strikes you as the most natural, the most authentic?

1) A child learns to play a video game by exploring it on his own.
2) A child learns to play a video game by watching a more experienced player.
3) A child learns to play a video game by being taught by a more experienced player.

In my experience a lot people take the first of these scenarios to be the most natural type of learning—we explore on our own. The third scenario has its place, but direct instruction from someone is a bit contrived compared to our own experience.

I’ve never really agreed with this point of view, simply because I don’t much care about “naturalness” one way or the other. As long as learning is happening, I’m happy, and I think the value some people place on naturalness is a hangover from a bygone Romantic era, as I describe here.

Now a fascinating paper by Patrick Shafto and his colleagues (2012) (that’s actually on a rather different topic) leads to implications that call into doubt the idea that exploratory learning is especially natural or authentic.

The paper focuses on a rather profound problem in human learning. Think of the vast difference in knowledge between a new born and a three-year-old; language, properties of physical objects, norms of social relations, and so on. How could children learn so much, so rapidly? 

As you're doubtless aware, from the 1920's through the 1960's, children were viewed by psychologists as relatively passive learners of their environment. More recently, infants and toddlers have been likened to scientists; they don't just observe the environment, they reason about what they observe.

But it's not obvious that reasoning will get the learning done. For example, in language the information available for their observation seems ambiguous. If a child overhears an adult comment “huh, look at that dog,” how is the child to know whether “dog” refers to the dog, the paws of the dog, to running (that the dog happens to be doing), to any object moving from the left to the right, to any multi-colored object etc.?

Much of the research on this problem has focused on the idea that there must be innate assumptions or biases on the part of children that help them make sense of their observations. For example, children might assume that new words they hear are more likely to apply to nouns than to adjectives.

Many models using these principles have not attached much significance to the manner in which children encounter information. Information is information.

Shafto et al. point out why that's not true. They draw a distinction between three different cases with the following example. You’re in Paris, and want a good cup of coffee.

1) You walk into a cafe, order coffee, and hope for the best.
2) You see someone who you know lives in the neighborhood. You see her buying coffee at a particular cafe so you get yours there too.
3) You see someone you know lives in the neighborhood. You see her buying coffee at a particular cafe. She sees you observing her, looks at her cup, looks at you, and nods with a smile

In the first case you acquire information on your own. There is no guiding principle behind this information acquisition. It is random, and learning where to find good coffee will slow going with this method.

In the second scenario, we anticipate that the neighborhood denizen is more knowledgeable than we--she probably knows where to get good coffee. Finding good coffee ought to be much faster if we imitate someone more knowledgeable than we. At the same time, there could be other factors at work. For example, it's possible that she thinks the coffee in that cafe is terrible, but it's never crowded and she's in a rush that morning.

In the third scenario, that's highly unlikely. The woman is not only knowledgeable, she communicates with us; she knows what we want to know and she can tell us that the critical feature we care about is present. Unlike scenario #2,  the knowledgeable person is adjusting her actions to maximize our learning. 

More generally, Shafto et al suggest that these cases represent three fundamentally different learning opportunities; learning from physical evidence, learning from the observation of goal-directed action, and learning from communication.

Shafto et al argue that although some learning theories assume that children acquire information at random, that's likely false much of the time. Kids are surrounded by people more knowledgeable than they. They can see, so to speak, where more knowledgeable people get their coffee.

Further, adults and older peers often adjust their behavior to make it easier for children to draw the right conclusion. Language is notable in its ambiguity-“dog” might refer to the object, its properties, its actions—but more knowledgeable others often do take into account what the child knows, and speak so as to maximize what the child can learn. If an adult asked “what’s that?”  I might say “It’s Westphalian ham on brioche.” If a toddler asked, I ‘d say “It’s a sandwich.”

One implication is that the problem I described—how do kids learn so much, so fast—may not be quite as formidable as it first seemed because the environment is not random. It has a higher proportion of highly instructive information. (The real point of the Shafto et al. paper is to introduce a Bayesian framework for integrating these different three types of learning scenarios into models of learning.)

The second implication is this: when a more knowledgeable person not only provides information but tunes the communication to the knowledge of the learner, that is, in an important sense, teaching.

So whatever value you attach to “naturalness,” bear in mind that much of what children learn in their early years of life may not be the product of unaided exploration of their environment, but may instead be the consequence of teaching. Teaching might be considered a quite natural state of affairs.

EDIT: Thanks to Pat Shafto who pointed out a paper (Csibra & Gergely) that draws out some of the "naturalness" implications re: social communication. 

Reference
Shafto, P., Goodman, N. D. & Frank, M. C. (2012). Learning from others: The consequences of psychological reasoning for human learning. Perspectives in Psychological Science, 7, 341-351.

If you read up on math pedagogy long enough you will see a reference to Paul Lockhart’s Mathematician’s Lament. It even has it’s own Wikipedia entry.

It is a marvelous little book of 140 pages, that makes a simple, 3 part argument about how to improve mathematics education the US.

Unfortunately, 89 pages of the book remains unwritten and it contains the third, decisive part of the argument.

The argument looks like this:

1)      Math as it is taught in the US is  boring

2)      Math doesn’t need to be boring. In fact, math is interesting and beautiful

3)      We can teach children the beauty and fascination of math in US schools by doing X.

Lockhart devotes 90 pages of the book to the first proposition, about 88 pages more, I estimate, than is necessary.

Lockhart suggests that the root of the problem lies in how teachers conceive or mathematics. Actually, it’s how everyone (save mathematicians) conceive of mathematics. We see it as a rigid, rule-based, practical. Lockhart offers mathematics as aesthetically pleasing problem solving. No more, no less. 

Mathematical ideas are inherently interesting, charming, fun. If you’re not interested, you’re doing math wrong—or being taught math wrong.

So why is math taught wrong?

Lockhart suggests that teaching math requires intense personal relationships with students, “choosing engaging and natural problems suitable to their tastes, personalities, and levels of experience,” and being flexible and open to the students’ shifts in curiosity. Lockhart doubts most teachers are interested in this sort of thing, and he suggests that most teachers see it as too much work (p. 44).

Later (p. 82) bureaucrats are blamed; they won’t allow individual teachers to follow their instincts. Later, we’re told more bluntly that schools ruin not just math, but all subjects.

But what of the third part of the argument in which Lockhart ought to tell us how make things better?

His vision of “better” is that teachers will pose interesting problems to students—he offers many compelling examples—and students will work on these problems under the guidance (ideally, the minimal guidance) of the teacher. The best learning, he avers, is where the student is doing math (i.e., creating arguments, finding patterns) rather than executing formulae described by others.

There is an irony here. Lockhart describes mathematical arguments as two-headed. One head is relentlessly logical, and rigidly insists that an argument be airtight. The other head has aesthetic criteria, and seeks an argument that is elegant, lovely, and that sheds light as it proves.

Lockharts prescription is all lovely and not enough logic.

For someone who excoriates a system that would allow people who don’t know the history of math to teach it, Lockhart is surprisingly quick to write about educational practice in the absence of any knowledge of its history.

Giving students interesting problems and aiding their efforts to solve them as the workhorse method of classroom learning—that idea has been mainstream for about 100 years. Further, surveys of teachers consistently show that they believe this method (and closely aligned methods) to be not only effective but desirable.

Teachers don’t fail to use these methods because they are lazy or because bureaucrats won’t let them.

These methods are really hard to pull off. Your knowledge of math needs to be very deep because the problem may pivot in an unexpected direction. Your classroom management needs to be flawless because you are expecting the students to work more independently.  And both knowledge of math and classroom management will be tapped further by the fact that you must make many decisions in the moment, as the classroom situation is very fluid.

The unfortunate thing about Mathematicians Lament is that Lockhart has put his finger on a real problem but is so caught up in righteous indignation that he loses the chance of doing any good. Simple scolding won’t do it. Jeremiah had compassion for the benighted in the Book of Lamentations.

A much more effective approach has been adopted by Hung-Hsi Wu, a mathematician at Berkeley. Wu has argued that a key problem is that today’s math teachers—products of the American system themselves—don’t get math. The solution is to teach them some math. (I once listened to a 30 minute explanation by Wu of why our system of whole numbers works the way it does. Quite literally, stuff that first graders can and should know. I was spellbound.)

In contrast to Lockhart, Wu has some faith in teachers. If they understand mathematics, they will teach it. He is also less dogmatic than Lockhart, who unthinkingly assumes that they only way to learn a topic is to practice it the way experts practice it. Indeed, some important elements that Lockhart wants to see—especially discovery—are present in some quite traditional approaches, especially the Japanese approach to teaching, as described by Jim Stigler.

Righteous indignation should be an occasional guilty pleasure, not a blueprint for math education.

Elsewhere I have written about the potential power of narrative to help students understand and remember complex subject matter (Willingham, 2004; 2009). Now a new study (Arya & Maul, 2012) provides fresh evidence that putting to-be-learned material in a story format improves learning outcomes.

The experiment tested 209 7th and 8th grade students in the U.S. on texts about the discoveries of Galileo OR the discoveries of Marie Curie. The texts were developed to be as similar as possible in terms of syntactic complexity, vocabulary, accuracy, and other measures, and vary only in whether the information was presented in a typical expository fashion or in terms of a personal story of the scientist.

For example, one section of the expository text included this passage

The corresponding passage in the narrative version read this way:

Students comprehension and memory for the information in the text was measured immediately after reading it, and again one week later. The difference in recall between the narrative and non-narrative versions are shown as difference scores below.

Science lends itself naturally to narrative structure--authors can tell the stories of individual scientists, their struggles, their discoveries, and so on.

There's a case to be made that it also lends itself to a triumphalist view of science that is not accurate; scientists as heroes in an ever-progressing march towards Truth. Since Kuhn, that more or less Popperian view of science has been viewed as at least too simple, and more likely inaccurate.

But if it helps middle schoolers understand science, I'm inclined not worry too much about that point.

Instead, I'd like to broaden the view of "narrative." (I made this point in Why Don't Students Like School.) You don't have to think of narrative just as the story of an individual or group of people; you can think more abstractly conflict, complications, and the eventual resolution of conflict as the core of narrative structure.

I prefer to think of narrative in this broader sense because it is more flexible, and gives teachers more options, and also better captures the aspects of narrative structure that I suspect are behind the advantage conferred.

Reference

  Arya, D. J. & Maul, A. (2012). The role of the scientific discovery narrative in middle school science education: An experimental study. Journal of Educational Psychology, 104, 1022-1032.